19. 删除链表的倒数第 N 个结点

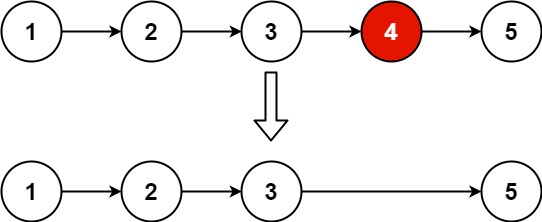
给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

1 2	输入：head = [1,2,3,4,5], n = 2 输出：[1,2,3,5]

示例 2：

1 2	输入：head = [1], n = 1 输出：[]

示例 3：

1 2	输入：head = [1,2], n = 1 输出：[1]

提示：

链表中结点的数目为 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz

**进阶：**你能尝试使用一趟扫描实现吗？

暴力做法

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        List<ListNode> list = new ArrayList<>();
        while(head != null){
            list.add(head);
            head = head.next;
        }
        int len = list.size();
        int x = len - n;
        list.remove(x);
        
        if (list.isEmpty()) {
            return null;
        }
        // 重新连接节点
        for (int i = 0; i < list.size() - 1; i++) {
            list.get(i).next = list.get(i + 1);
        }
        list.get(list.size() - 1).next = null; // 确保最后一个节点的next为null
        return list.get(0);

    }
}

📖 文字题解

前言

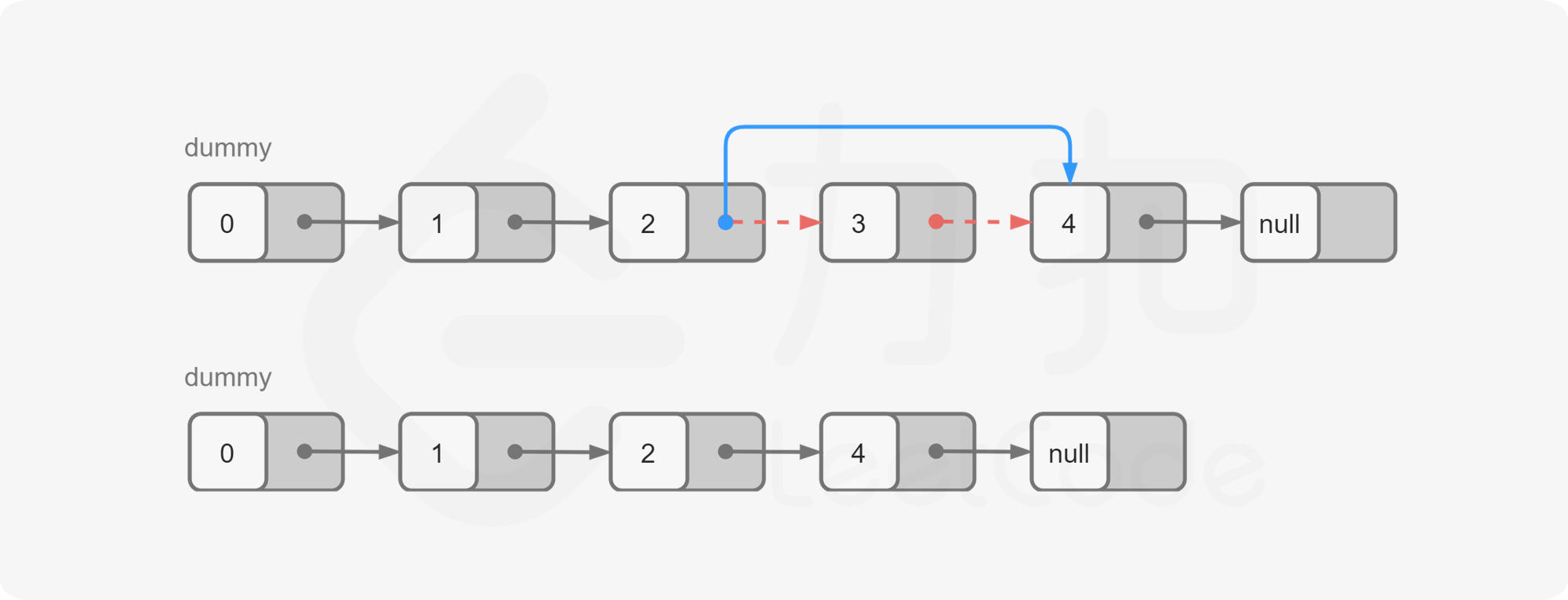
在对链表进行操作时，一种常用的技巧是添加一个哑节点（dummy node），它的 next 指针指向链表的头节点。这样一来，我们就不需要对头节点进行特殊的判断了。

例如，在本题中，如果我们要删除节点 y，我们需要知道节点 y 的前驱节点 x，并将 x 的指针指向 y 的后继节点。但由于头节点不存在前驱节点，因此我们需要在删除头节点时进行特殊判断。但如果我们添加了哑节点，那么头节点的前驱节点就是哑节点本身，此时我们就只需要考虑通用的情况即可。

特别地，在某些语言中，由于需要自行对内存进行管理。因此在实际的面试中，对于「是否需要释放被删除节点对应的空间」这一问题，我们需要和面试官进行积极的沟通以达成一致。下面的代码中默认不释放空间。

方法一：计算链表长度

思路与算法

一种容易想到的方法是，我们首先从头节点开始对链表进行一次遍历，得到链表的长度 L。随后我们再从头节点开始对链表进行一次遍历，当遍历到第 L−n+1 个节点时，它就是我们需要删除的节点。

为了与题目中的 n 保持一致，节点的编号从 1 开始，头节点为编号 1 的节点。

为了方便删除操作，我们可以从哑节点开始遍历 L−n+1 个节点。当遍历到第 L−n+1 个节点时，它的下一个节点就是我们需要删除的节点，这样我们只需要修改一次指针，就能完成删除操作。

代码

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(0, head);
        int length = getLength(head);
        ListNode cur = dummy;
        for (int i = 1; i < length - n + 1; ++i) {
            cur = cur.next;
        }
        cur.next = cur.next.next;
        ListNode ans = dummy.next;
        return ans;
    }

    public int getLength(ListNode head) {
        int length = 0;
        while (head != null) {
            ++length;
            head = head.next;
        }
        return length;
    }
}

复杂度分析

时间复杂度：O(L)，其中 L 是链表的长度。
空间复杂度：O(1)。

方法二：栈

思路与算法

我们也可以在遍历链表的同时将所有节点依次入栈。根据栈「先进后出」的原则，我们弹出栈的第 n 个节点就是需要删除的节点，并且目前栈顶的节点就是待删除节点的前驱节点。这样一来，删除操作就变得十分方便了。

代码

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(0, head);
        Deque<ListNode> stack = new LinkedList<ListNode>();
        ListNode cur = dummy;
        while (cur != null) {
            stack.push(cur);
            cur = cur.next;
        }
        for (int i = 0; i < n; ++i) {
            stack.pop();
        }
        ListNode prev = stack.peek();
        prev.next = prev.next.next;
        ListNode ans = dummy.next;
        return ans;
    }
}

复杂度分析

时间复杂度：O(L)，其中 L 是链表的长度。
空间复杂度：O(L)，其中 L 是链表的长度。主要为栈的开销。

方法三：双指针

思路与算法

我们也可以在不预处理出链表的长度，以及使用常数空间的前提下解决本题。

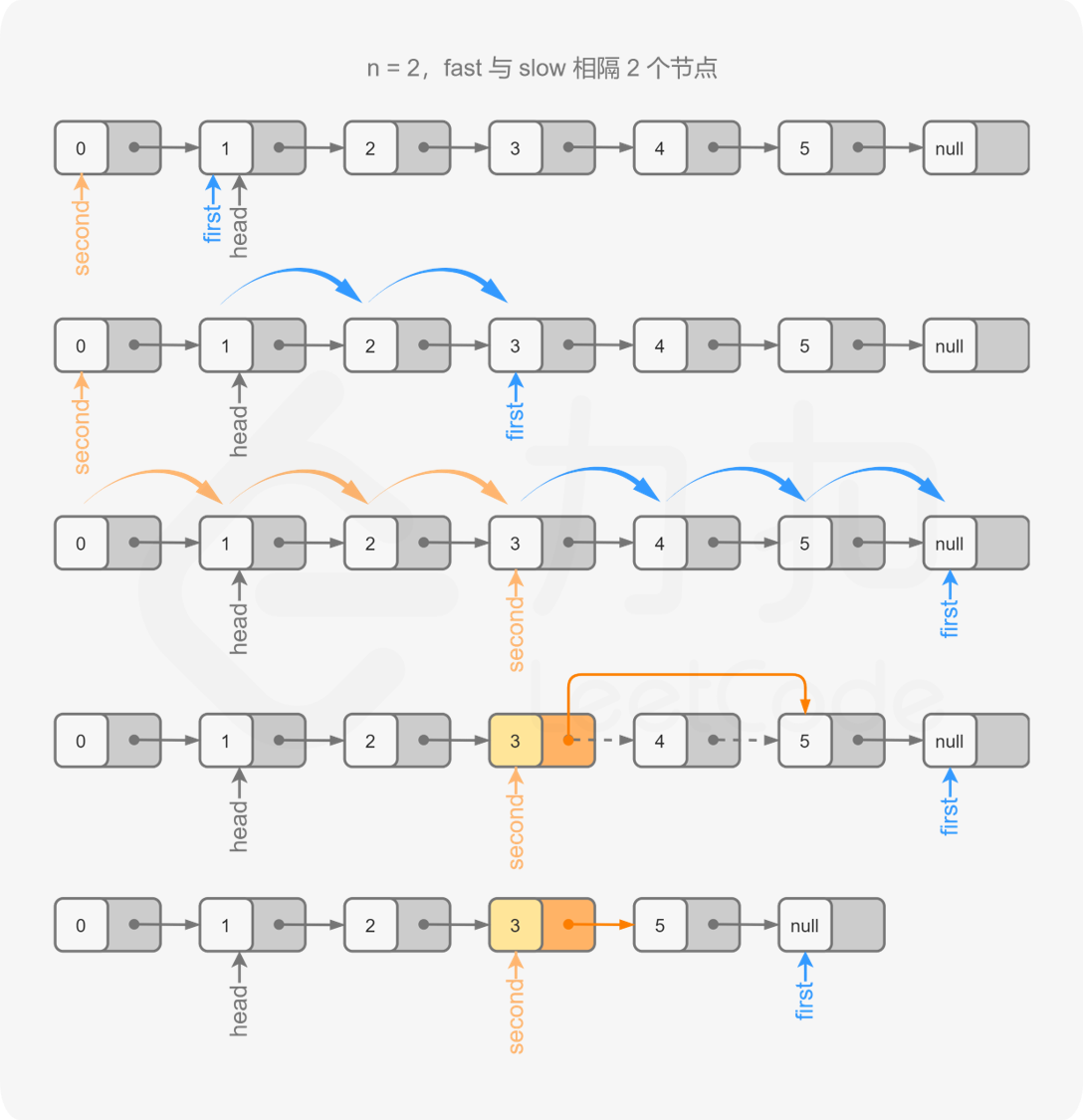
由于我们需要找到倒数第 n 个节点，因此我们可以使用两个指针 first 和 second 同时对链表进行遍历，并且 first 比 second 超前 n 个节点。当 first 遍历到链表的末尾时，second 就恰好处于倒数第 n 个节点。

具体地，初始时 first 和 second 均指向头节点。我们首先使用 first 对链表进行遍历，遍历的次数为 n。此时，first 和 second 之间间隔了 n−1 个节点，即 first 比 second 超前了 n 个节点。

在这之后，我们同时使用 first 和 second 对链表进行遍历。当 first 遍历到链表的末尾（即 first 为空指针）时，second 恰好指向倒数第 n 个节点。

根据方法一和方法二，如果我们能够得到的是倒数第 n 个节点的前驱节点而不是倒数第 n 个节点的话，删除操作会更加方便。因此我们可以考虑在初始时将 second 指向哑节点，其余的操作步骤不变。这样一来，当 first 遍历到链表的末尾时，second 的下一个节点就是我们需要删除的节点。

代码

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(0, head);
        ListNode first = head;
        ListNode second = dummy;
        for (int i = 0; i < n; ++i) {
            first = first.next;
        }
        while (first != null) {
            first = first.next;
            second = second.next;
        }
        second.next = second.next.next;
        ListNode ans = dummy.next;
        return ans;
    }
}

复杂度分析

时间复杂度：O(L)，其中 L 是链表的长度。
空间复杂度：O(1)。